حقایقی شگفت انگیز در ریاضیات

وب سایت ایکس تی آی: ریاضیات برای شما حقایقی شگفت انگیز را برای امتحان محدودیت ذهنی شما آماده کرده است. آنها تناقضات و خصیصه های ذاتی احتمال هستند. اگر شما دنبال یک راه حل ریاضی برای تحت تاثیر قرار دادن دوستان و فریب دادن دشمنان خود هستید؛ اینجا یک مکان عالی برای شروع است!

۱.پارادوکس تاریخ تولد

فرض کنید شما در یک اداره‌ی ۲۳ نفری هستید. با فرض اینکه هیچ‌کس نمی‌تواند متولد ۳۰ اسفند باشد؛ احتمال آن که دو نفر در اداره‌ی شما تاریخ تولد یکسانی داشته باشند چه قدر است؟ در یک اداره ۵۷ نفره چطور؟

جواب: در بین ۲۳ نفر ۵۰ درصد و در بین ۵۷ نفر ۹۹ درصداحتمال وجود دارد که دو نفر تاریخ تولد یکسانی داشته باشند.

حتماً می‌دانبد که بنابر اصل لانه کبوتری، در صورتی که جمعیت اداره به ۳۶۶ نفر برسد، حداقل دو نفر تاریخ تولد یکسانی خواهند داشت. هرچند، باور اینکه در یک اداره ۵۷ نفری به احتمال ۹۹ درصد دو نفر تاریخ تولد یکسانی داشته باشند کمی سخت است.
اصل لانه کبوتری بیان می‌کند که اگر دو عدد طبیعی n و m را با خاصیت n> m داشته باشیم، اگر n شیء در m لانه کبوترقرار گیرد، آن‌گاه حداقل یک لانه کبوتر (یا قفسه) دارای بیش از یک شیء خواهد بود. در واقع اضافه کردن یک شیء دیگر ما را مجبور می‌کند که از یکی از لانه‌ها بار دیگر استفاده کنیم (با این شرط که m متناهی باشد). در اینجا ما جمعیت را n و تعداد روز‌های سال را m در نظر می‌گیریم.

اما چگونه به این جواب رسیدیم؟

بیایید به اداره‌ی ۲۳ نفری برگردیم تا ببینیم چگونه چنین چیزی امکان پذیر است. ما برای محاسبه این مقدار برای آسان تر شدن محاسبه از روش اصل متمم (احتمال قرار نگرفتن تاریخ تولد دو نفر در یک روز یکسان) استفاده خواهیم کرد. در برخی از پرسش‌های شمارشی، شمردن حالت‌های نا مطلوب از مطلوب ساده تر است. برای حل این پرسش‌ها در اکثر اوقات از اصل متمم استفاده می‌کنیم. بنابراین احتمال اینکه دو نفر تاریخ تولد یکسانی نداشته باشند، اینگونه محاسبه می‌شود:


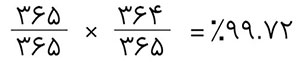
و احتمال اینکه سه نفر تاریخ تولد یکسان نداشته باشند:


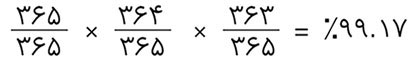
و همچنین چهار نفر:


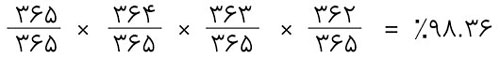
بدین جهت، بیست و سه نفری که تاریخ تولد یکسانی ندارند ۴۹.۲۷ درصد است:


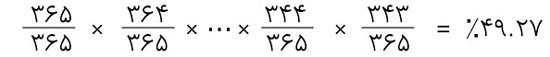
این بدین معنی است ۵۰.۷ درصد (۵۰.۷=۴۹.۳ - ۱۰۰) احتمال وجود دارد که حداقل دو نفر تاریخ تولد یکسانی داشته باشند.


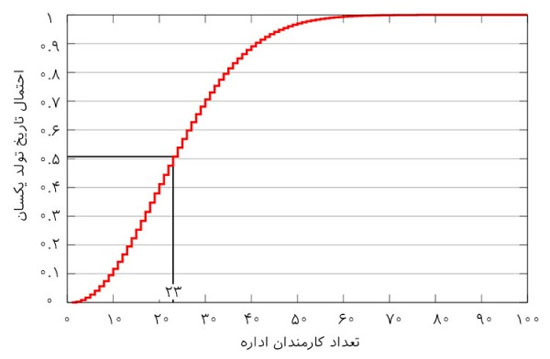
جالب است بدانید که اگر تعداد افراد به ۷۵ نفر برسد، به احتمال ۹۹.۹درصد دو نفر دارای تاریخ تولد یکسان خواهند بود.


۲. قانون بنفورد

در ۳۰ درصد موارد رقم اول اعدادی که در جهان با آن مواجه می‌شویم، عدد «۱» است.

قانون بِنفورد یا قانون رقم اول می‌گوید که در فهرست عددهایی که در بسیاری از (البته نه همهٔ) پدیده‌های زندگی واقعی رخ می‌دهند، رقم اول عددها به طور خاص و غیریکنواختی توزیع می‌شود. بر طبق این قانون، تقریباً در یک‌سوم موارد رقم نخست ۱ است، و عددهای بزرگ‌تر در رقم نخست به ترتیب با بسامد کمتری رخ می‌دهند، و عدد ۹ کمتر از یک بار در هر بیست عدد ظاهر می‌شود.این موضوع توسط فرانک بنفورد فیزیکدان در سال ۱۹۳۸ کشف شد. میزان ظاهر شدن بقیه‌ی اعداد در رقم اول نیز توزیع لگاریتمی به شکل زیر دارد:


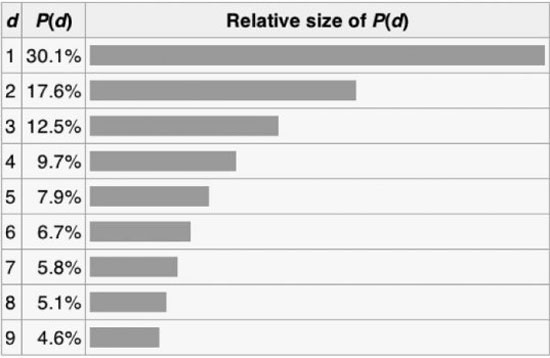
از قانون بنفورد برای صحت نتایج به دست آمده انتخابات، اطلاعات مالی، حسابرسی‌های قانونی و … استفاده می‌کنند. چرا که اگر حساب‌ها با قانون بنفورد مطابقت نداشته باشند به این معنی خواهد بود که حساب‌ها و اعداد به احتمال فراوان جعلی هستند.

همچنین در دنباله‌ی اعداد فیبوناجی:

{… ۳۴ و ۲۱ و ۱۳ و ۸ و ۵ و ۳ و ۲ و ۱ و ۱}

فاکتوریل و مجموعه‌ی توان‌های عدد ۲ نیز قانون بنفورد دیده می‌شود.

این قانون به ظاهر عجیب در بسیاری از داده‌ها برقرار است، مثلاً در صورتحساب‌های برق، شمارهٔ خیابان‌ها، قیمت سهام، مقدار جمعیت، آمار مرگ‌ومیر، طول رودخانه‌ها، ثابت‌های فیزیک و ریاضیات، و فرایندهایی که از توزیع توانی پیروی می‌کنند (که در طبیعت بسیار فراوانند). این قانون مستقل از پایه‌ای که عددها در آن بیان می‌شوند برقرار است، هرچند که احتمال تکرار عددها در هر پایه متفاوت از پایه‌های دیگر است. اگر چه قانون بنفورد قطعاً در بسیاری از مواقع به صورت شهودی صدق می‌کند ، اما توضیح علمی آن در سال ۱۹۹۸ توسط هیل، ریاضیدان، با استفاده از قضایای حد مرکزی-گونه داده شده‌است.در حقیقت تا پیش از سال ۱۹۹۶ هیچ‌کس نتوانست علت قانون بنفورد را به درستی توضیح دهد.


۳. …۰.۹۹۹ برابر ۱ است!

راه‌های زیادی برای اثبات این حقیقت که…۰.۹۹۹=۱ است وجود دارد، اما همچنان برخی از مردم ایم موضوع را رد می‌کنند. برای مثال، اثبات زیر به خوبی این قضیه را نشان می‌دهد:

x = 0.999…

10x = 9.999…

10x - x = 9.999… - 0.999…

9x = 9

x = 1

یکی از دلایلی که سبب می‌شود مردم این قضیه را متوجه نشوند، نداشتن فهم درستی از مفهوم بی‌نهایت است. برخی‌ها تصور می‌کنند در نهایت این نقطه چین‌ها بالاخره به یک عدد 9 نهایی ختم می‌شوند در حالی که این طور نیست. اعداد را می‌توان به شکل‌های متفاوت نمایش داد که در اینجا …۰.۹۹۹ شکل دیگری از عدد یک است. دلیل این موضوع ارتباط نزدیکی با مفهوم حد و بی‌نهایت در ریاضیات دارد. اگر اثبات بالا برای شما کافی نبود، می‌توانید از این اثبات ساده تر استفاده کنید:

⅓ = 0.333…

3 * ⅓ = 3 * 0.333…

1 = 0.999…


۴. معمای مانتی هال

بگذارید بگوییم که شما در یک نمایش تلویزیونی هستید و مجری برنامه به شما سه درب نشان می‌دهد، پشت یکی از درب ها یک ماشین آخرین مدل و پشت درب ‌های دیگر دو بز قرار دارد. هنگامی که شما یک درب را انتخاب می‌کنید، مجری یکی از دو دربی که انتخاب نکرده بودید را باز می‌کند تا یکی از بز‌ها را مشاهده کنید.

مجری از شما می‌پرسد که آیا مایل به تغییر دادن درب انتخابی هستید؟ یا اینکه می‌خواهید همان انتخاب اولتان پابرجا باشد؟شما چه کاری انجام خواهید داد؟

اگر فکر می‌کنید که چون دو درب باقی مانده و شانس شما برای هر پنجاه درصد است؛ شما در اشتباه هستید! بهترین استراتژی برای پیروزی تغییر دربی است که بار اول انتخاب نموده‌اید. اما چگونه چنین چیزی ممکن است؟

احتمال انتخاب دربی که پشت آن ماشین قرار دارد در اولین حرکت ۱/۳ است. از طرفی شانس باخت در صورت تعویض درب هم ۱/۳ است. بنابراین کسی که درب انتخابی اش را تغییر دهد، ۲/۳ شانس پیروزی دارد؛ یعنی دو برابر حالت اول که درب انتخابی را تغییر نداده‌اید. توجه داشته باشید که مکان ماشین در پشت درب ها ثابت است و از دلایلی که باعث می‌شود شانس پیروزی با تغییر درب بیشتر شود همین مورد است.

اگر درب شماره یک را انتخاب کنید؛ جدول زیر تمام حالات ممکن را نشان می‌دهد:

اگر درب انتخابی خود را عوض نکنید، از هر سه بار، تنها یک بار برنده می‌شوید، در حالی که در صورت تعویض درب، دو بار در هر سه بار برنده خواهید شد.

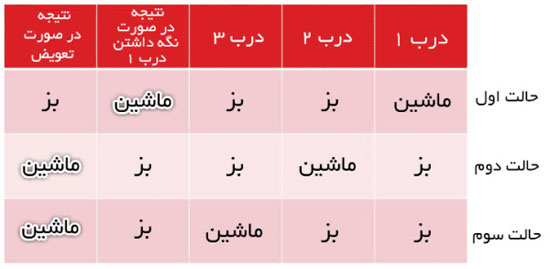
هنوز در درستی این مطلب تردید دارید؟ این بار مسئله را با ۵۰ درب در نظر بگیرید و فرض کنید که درب اول را انتخاب نموده‌اید. مجری با باز کردن ۴۸ درب، ۴۸ بز به شما نشان خواهد داد!


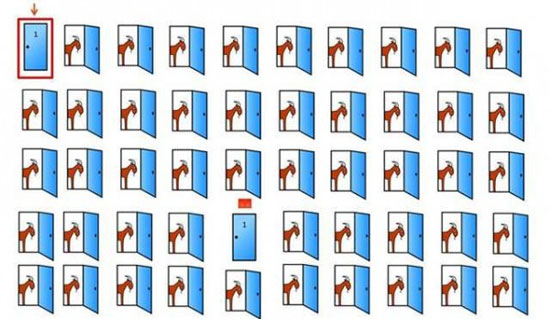
البته تمامی توضیحات بالا تنها در صورتی درست خواهند بود که شما قصد بردن ماشین را داشته باشید و نه بز را!


۵. تخمین عدد پی با رسم یک مربع و یک دایره و تعدادی دانه‌ی شنروش مونت کارلو در محاسبه عدد پی

دایره‌ای به شعاع r را درون مربعی به ضلع 2r محاط کنید. در این صورت مساحت دایره برابر πr2 و مساحت مربع برابر 4r2 خواهد شد. در ادامه چندین شکل با اندازه یکسان (برای مثال، دانه‌های شن یا برنج) را در سرتاسر مربع روی آن به طور یکنواخت پخش کنید.

سپس تعداد اشیاء درون دایره را بشمارید، در چهار ضرب کنید و عدد به دست آمده را بر تعداد کل اشیاء درون مربع تقسیم نمایید.

نسبت اشیاء درون دایره در مقابل اشیاء درون مربع تقریباً برابر خواهد بود با ۴/π، که همان نسبت سطح دایره‌است به سطح مربع؛ بنابراین شما تخمینی از عدد π را به دست آورده‌اید.



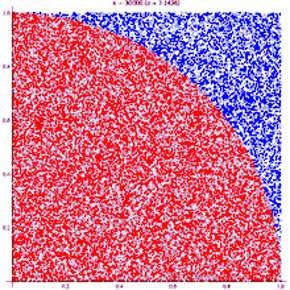
این روش، به روش مونت کارلو مشهور است. به طور کلی این روش به محاسبات آماری که با نمونه‌گیری تصادفی همراه است اطلاق می‌شود.

توجه داشته باشید که روش فوق زمانی بهترین جواب را می‌دهد که:

محل قرار گیری دانه‌های شن کاملاً تصادفی باشند.

تعداد دانه‌ها زیاد باشد.