بحث برانگیزترین معماهای ریاضی (۲)
گاهی اوقات در ریاضیات با مسائل و معماهایی روبرو میشویم که در نگاه اول به نظر میرسد پاسخ آنها با «عقل سلیم» در تضاد باشد.
zoomit.ir - مسعود توکلی: گاهی اوقات در ریاضیات با مسائل و معماهایی روبرو میشویم که در نگاه اول به نظر میرسد پاسخ آنها با «عقل سلیم» در تضاد باشد. در قسمت قبل با چند مورد از این حقایق ریاضی که حتی افراد باهوش هم در درک آن دچار مشکل هستند، آشنا شدیم.

۵. مسئلهی تاریخ تولد
فرض کنید در یک اداره کار میکنید که در مجموع ۲۳ کارمند دارد. احتمال اینکه دو نفر از کارمندان تاریخ تولد یکسانی داشته باشند چقدر است؟ (در این مسئله با فرض اینکه هیچکس نمیتواند متولد ۳۰ اسفند باشد، از سالهای کبیسه صرف نظر میکنیم.) در صورتی که تعداد کارمندان اداره ۵۷ نفر باشد، این احتمال چقدر خواهد بود؟

به احتمال زیاد از قبل میدانید هنگامی که جمعیت یک اداره به ۳۶۶ نفر برسد، بنا به اصل لانهی کبوتر (و با توجه به فرض مسئله) به احتمال ۱۰۰ درصد حداقل دو نفر تاریخ تولد یکسانی خواهند داشت. این حقیقت ممکن است منجر به این باور غلط شود که احتمال وجود افراد با تاریخهای تولد یکسان در حالت اول کمتر از ۱۰ درصد و در حالت دوم حدود ۱۵ درصد است.
اما پاسخ صحیح مسئله در حالت اول (۲۳ کارمند) ۵۰ درصد، و در حالت دوم (۵۷ کارمند) ۹۹ درصد است!
شاید باور اینکه در یک ادارهی ۲۳ نفره به احتمال ۵۰ درصد دو نفر تاریخ تولد یکسانی داشته باشند کمی سخت باشد. از آن سختتر باور کردن احتمال ۹۹ درصدی وجود تاریخ تولد یکسان در یک ادارهی ۵۷ نفره است. اما این احتمالات قابل اثبات هستند.
از ادارهی ۲۳ نفری شروع کنیم:
برای اثبات پاسخ این مسئله، از احتمال معکوس یا converse probability (احتمال قرار نگرفتن تاریخ تولد دو نفر در یک روز یکسان) استفاده میکنیم؛ چرا که محاسبهی احتمال به روش مستقیم در این مسئله کار بسیار مشکلی است. احتمال اینکه دو نفر تاریخ تولد یکسانی نداشته باشند، اینگونه محاسبه میشود.
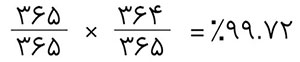
این احتمال برای ۳ نفر به این صورت به دست میآید:
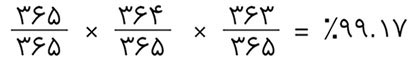
همچنین برای ۴ نفر داریم:
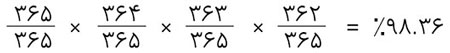
با ادامهی این روش تا ۲۳ نفر خواهیم داشت:
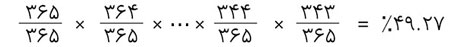
این یعنی از آنجایی که ۴۹.۳% احتمال دارد هیچکس تاریخ تولد یکسانی با کس دیگری نداشته باشد، پس ۵۰.۷% احتمال وجود دارد که حداقل دو نفر در این ادارهی ۲۳ نفره تاریخ تولد یکسانی داشته باشند.
در حالت دوم مسئله هم با استفاده از همین روش به احتمال ۹۹ درصد میرسیم. جالب است بدانید در صورتیکه تعداد کارمندان به ۷۵ نفر برسد، احتمال یکسان بودن تاریخ تولدها به ۹۹.۹ درصد میرسد.
نمودار احتمال این مسئله به شکل زیر است:
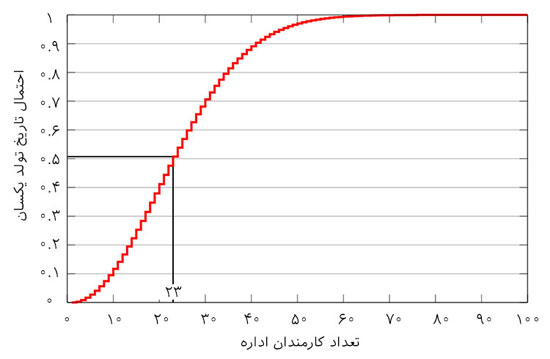
در اینجا میتوانید علاوه بر آشنایی بیشتر با این مسئله و مطالعهی اثباتهای دقیق ریاضی، با استفاده از شبیهساز سایت، خودتان احتمالات را با هر تعداد دلخواه کارمند به صورت شهودی بررسی کنید.
۶. پارادوکس جعبهی برتراند
فرض کنید ۳ جعبه وجود دارد که هر کدام از آنها دارای دو محفظه هستند. در یکی از جعبهها دو شمش طلا، در دیگری دو شمش نقره و در جعبهی سوم یک شمش طلا و یک شمش نقره قرار دارد.
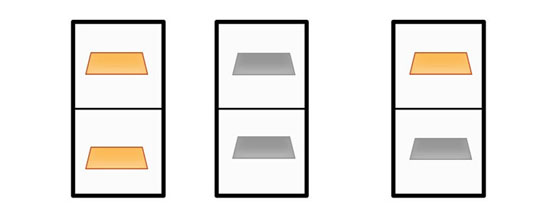
یک جعبه را به صورت تصادفی انتخاب کرده و یکی از محفظههای آن را (آن هم به صورت تصادفی) باز میکنید. اگر شمشی که به دست آورده باشید از جنس طلا باشد، احتمال اینکه شمش درون محفظهی دیگر همان جعبه هم از جنس طلا باشد چقدر است؟

پاسخی که در ابتدا به ذهن اکثر افراد میرسد این است:
از آنجایی که تنها دو جعبه با شمش طلا وجود دارد، حتماً یکی از آنها را انتخاب کردهام. همچنین از آنجایی که یکی از این دو جعبه در محفظه دیگر خود شمش نقره، و دیگری شمش طلا دارد، پس حتماً پاسخ مسئله ۵۰ درصد است.
این پاسخ اشتباه است.
برای اینکه بهتر متوجه شویم چرا احتمال طلا بودن شمش دیگر ۵۰ درصد نیست، شمشها را به این صورت نامگذاری میکنیم.

حال بیایید همهی حالات ممکن را با هم بررسی کنیم.
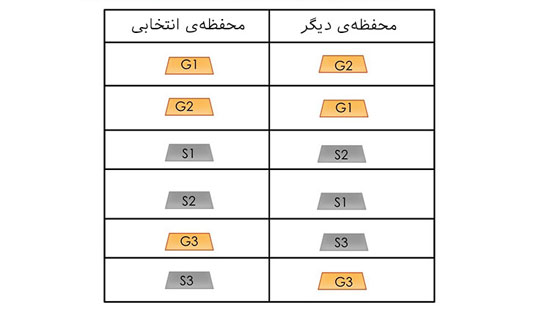
سپس تنها حالاتی را که در آنها انتخاب اول شما شمش طلا بوده است را در نظر میگیریم.
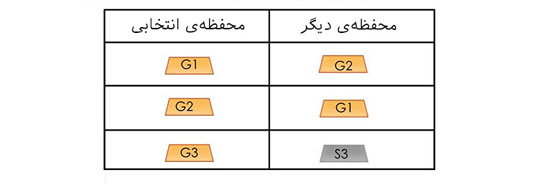
همانطور که مشخص است، اگر در انتخاب اول با شمش طلا مواجه شوید، به احتمال دو سوم شمش محفظهی دیگر نیز از جنس طلا است.
این معما رابطهی تنگاتنگی با معمای مانتی هال دارد. اگر استدلالهای معمای مانتی هال شما را قانع نکرده است، احتمالاً پاسخ این مسئله را هم به سادگی نخواهید پذیرفت.
در هر صورت اگر علاقهمند به مطالعهی بیشتر دربارهی این مسئله هستید، میتوانید به اینجا و اینجا مراجعه کنید.
۷. معمای هتل هیلبرت

هتلی را در نظر بگیرید که «بینهایت» اتاق دارد و تمامی اتاقهای آن پُر است. مسافر جدیدی از راه میرسد و مدیریت هتل به او میگوید که یک اتاق خالی برای او سراغ دارد. با توجه به پُر بودن تمامی اتاقها، مدیر هتل چگونه قرار است برای مسافر اتاق خالی پیدا کند؟
پاسخ معما به این صورت است:
از آنجایی که تمام اتاقهای هتل پر از مسافر است، مدیر هتل از مسافر اتاق ۱ میخواهد تا به اتاق شماره ۲ نقل مکان کند. همچنین از مسافر اتاق ۲ نیز درخواست میکند تا به اتاق شماره ۳ تغییر مکان بدهد.
همینطور مسافر اتاق ۳ به ۴، ۴ به ۵، ۵ به ۶ و ... . در واقع مدیر هتل از مسافر اتاق n تقاضا میکند تا به اتاق n + ۱ برود. از آنجایی که هتل بینهایت اتاق دارد، همواره اتاقی برای انتقال مسافران وجود خواهد داشت. با این کار اتاق ۱ خالی میشود و مسافر جدید میتواند در آن اسکان بیابد.
اگر شب بعد یک اتوبوس ۶۰ نفری برای هتل میهمان بیاید چطور؟ این بار آقای مدیر چه ترفندی برای اسکان مسافران جدید در هتلِ کاملاً پرِ خود به کار خواهد گرفت؟
این دفعه مدیریت هتل از مسافر اتاق ۱ میخواهد تا به اتاق ۶۱ برود. همینطور مسافر اتاق ۲ به اتاق ۶۲، ۳ به ۶۳، ۴ به ۶۴ و ... . به این ترتیب ۶۰ اتاق اول هتل خالی خواهند شد. احتمالاً قاعدهی جای دادن n تعداد (متناهی) مسافر در این هتل را حدس زده باشید؛ برای اسکان m مسافر جدید، مسافر اتاق n را به اتاق n+m انتقال میدهیم.
اما اگر شب بعد اتوبوسی با «بینهایت» مسافر جدید از راه برسد، چطور میتوان آنها را در هتلی که حتی یک اتاق خالی هم ندارد جای داد؟
شیوهی حل مسئله این بار به این صورت است که از مسافر اتاق ۱ درخواست میکنیم به اتاق۲ برود، مسافر اتاق ۲ به اتاق ۴، ۳ به ۶، ۴ به ۸ و ... . یعنی مسافران اتاقهای n به اتاقهای ۲n نقل مکان کنند. با این کار اتاقهای ۲n-۱ (فرد) که تعدادشان بینهایت است، آمادهی پذیرایی از بینهایت مسافر جدید خواهند بود.
درک این مسئله و راه حل آن نیز رابطهی تنگاتنگی با درک مسئلهی ۲ در قسمت قبل این مجموعه دارد. دانستن مفاهیم «تناظر یک به یک» و «مجموعههای نامتناهیِ قابل شمارش» به شما در فهم راه حل این مسئله کمک خواهد کرد.
در حقیقت حتی اگر بینهایت اتوبوس که هر کدام بینهایت مسافر دارند هم از راه برسند، میتوان آنها را در هتل جای داد. اثبات این حالت کمی پیچیدهتر از حالات قبلی است و اگر علاقه دارید میتوانید در اینجا و اینجا دربارهی آن بیشتر بخوانید.
۸. چگونه میتوان با استفاده از تختهی دارت، مقدار π (عدد پی) را تخمین زد؟
یکی از جالبترین راهها برای تخمین مقدار π، انتخاب تصادفی نقاط در شکل زیر است.
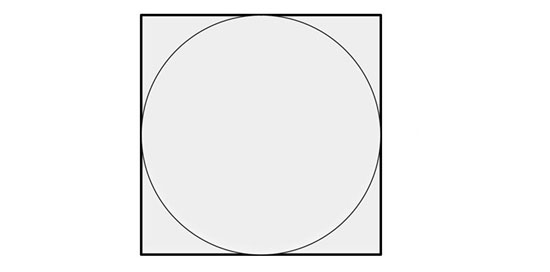
چنین شکلی را خودتان هم میتوانید با هر ابعاد دلخواهی درست کنید. فرض کنیم شعاع دایره برابر r باشد. در نتیجه قطر مربعی که آن را محاط کرده است برابر ۲r است. با این حساب مساحت دایره πr۲ و مساحت مربع ۴r۲ خواهد بود.
نسبت مساحت دایره به مربع نیز برابر π چهارم میشود. حالا به هر روشی که دوست دارید، به صورت تصادفی نقاطی را بر روی صفحهی فوق انتخاب کنید.
دقت داشته باشید که هیچ عاملی به جز شانس در انتخاب نقاط دخیل نباشد. هر چقدر که تعداد این نقاط تصادفی بیشتر باشد، نسبت نقاطی که درون دایره قرار گرفتهاند به نقاط خارج از دایره (و درون مربع) به عدد π چهارم نزدیکتر خواهد شد. مقدار تقریبی π با استفاده از این روش، اینگونه حساب میشود.

البته باید توجه داشت که صورت مسئله ممکن است کمی گمراه کننده باشد، چرا که در شرایط پرتاپ دارت به سوی بورد، ممکن است عوامل دیگری نیز دخیل باشند که توزیع تصادفی نقطهها بر روی شکل را تحت تاثیر قرار بدهند؛ اما باید در نظر داشت که عنوان معماها صرفاً برای ساده سازی، رساندن مفهوم کلی و جذابتر کردن مسئله طراحی میشوند. صورت مسئله تعریف دقیقتری را ارائه میدهد.
به طور کلی، این نوع محاسبات آماری که با نمونهگیری تصادفی همراه است، به روش مونته کارلو (Monte Carlo method) مشهور است. دربارهی محاسبهی مقدار π به صورت آماری میتوانید در اینجا به مطالعه بپردازید.

فرض کنید در یک اداره کار میکنید که در مجموع ۲۳ کارمند دارد. احتمال اینکه دو نفر از کارمندان تاریخ تولد یکسانی داشته باشند چقدر است؟ (در این مسئله با فرض اینکه هیچکس نمیتواند متولد ۳۰ اسفند باشد، از سالهای کبیسه صرف نظر میکنیم.) در صورتی که تعداد کارمندان اداره ۵۷ نفر باشد، این احتمال چقدر خواهد بود؟

اما پاسخ صحیح مسئله در حالت اول (۲۳ کارمند) ۵۰ درصد، و در حالت دوم (۵۷ کارمند) ۹۹ درصد است!
شاید باور اینکه در یک ادارهی ۲۳ نفره به احتمال ۵۰ درصد دو نفر تاریخ تولد یکسانی داشته باشند کمی سخت باشد. از آن سختتر باور کردن احتمال ۹۹ درصدی وجود تاریخ تولد یکسان در یک ادارهی ۵۷ نفره است. اما این احتمالات قابل اثبات هستند.
از ادارهی ۲۳ نفری شروع کنیم:
برای اثبات پاسخ این مسئله، از احتمال معکوس یا converse probability (احتمال قرار نگرفتن تاریخ تولد دو نفر در یک روز یکسان) استفاده میکنیم؛ چرا که محاسبهی احتمال به روش مستقیم در این مسئله کار بسیار مشکلی است. احتمال اینکه دو نفر تاریخ تولد یکسانی نداشته باشند، اینگونه محاسبه میشود.
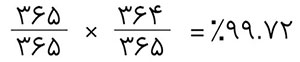
این احتمال برای ۳ نفر به این صورت به دست میآید:
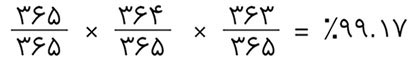
همچنین برای ۴ نفر داریم:
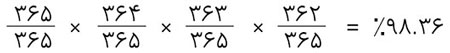
با ادامهی این روش تا ۲۳ نفر خواهیم داشت:
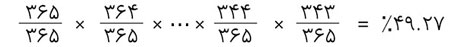
این یعنی از آنجایی که ۴۹.۳% احتمال دارد هیچکس تاریخ تولد یکسانی با کس دیگری نداشته باشد، پس ۵۰.۷% احتمال وجود دارد که حداقل دو نفر در این ادارهی ۲۳ نفره تاریخ تولد یکسانی داشته باشند.
در حالت دوم مسئله هم با استفاده از همین روش به احتمال ۹۹ درصد میرسیم. جالب است بدانید در صورتیکه تعداد کارمندان به ۷۵ نفر برسد، احتمال یکسان بودن تاریخ تولدها به ۹۹.۹ درصد میرسد.
نمودار احتمال این مسئله به شکل زیر است:

در اینجا میتوانید علاوه بر آشنایی بیشتر با این مسئله و مطالعهی اثباتهای دقیق ریاضی، با استفاده از شبیهساز سایت، خودتان احتمالات را با هر تعداد دلخواه کارمند به صورت شهودی بررسی کنید.
۶. پارادوکس جعبهی برتراند
فرض کنید ۳ جعبه وجود دارد که هر کدام از آنها دارای دو محفظه هستند. در یکی از جعبهها دو شمش طلا، در دیگری دو شمش نقره و در جعبهی سوم یک شمش طلا و یک شمش نقره قرار دارد.

یک جعبه را به صورت تصادفی انتخاب کرده و یکی از محفظههای آن را (آن هم به صورت تصادفی) باز میکنید. اگر شمشی که به دست آورده باشید از جنس طلا باشد، احتمال اینکه شمش درون محفظهی دیگر همان جعبه هم از جنس طلا باشد چقدر است؟

پاسخی که در ابتدا به ذهن اکثر افراد میرسد این است:
از آنجایی که تنها دو جعبه با شمش طلا وجود دارد، حتماً یکی از آنها را انتخاب کردهام. همچنین از آنجایی که یکی از این دو جعبه در محفظه دیگر خود شمش نقره، و دیگری شمش طلا دارد، پس حتماً پاسخ مسئله ۵۰ درصد است.
این پاسخ اشتباه است.
برای اینکه بهتر متوجه شویم چرا احتمال طلا بودن شمش دیگر ۵۰ درصد نیست، شمشها را به این صورت نامگذاری میکنیم.

حال بیایید همهی حالات ممکن را با هم بررسی کنیم.

سپس تنها حالاتی را که در آنها انتخاب اول شما شمش طلا بوده است را در نظر میگیریم.

همانطور که مشخص است، اگر در انتخاب اول با شمش طلا مواجه شوید، به احتمال دو سوم شمش محفظهی دیگر نیز از جنس طلا است.
این معما رابطهی تنگاتنگی با معمای مانتی هال دارد. اگر استدلالهای معمای مانتی هال شما را قانع نکرده است، احتمالاً پاسخ این مسئله را هم به سادگی نخواهید پذیرفت.
در هر صورت اگر علاقهمند به مطالعهی بیشتر دربارهی این مسئله هستید، میتوانید به اینجا و اینجا مراجعه کنید.
۷. معمای هتل هیلبرت

هتلی را در نظر بگیرید که «بینهایت» اتاق دارد و تمامی اتاقهای آن پُر است. مسافر جدیدی از راه میرسد و مدیریت هتل به او میگوید که یک اتاق خالی برای او سراغ دارد. با توجه به پُر بودن تمامی اتاقها، مدیر هتل چگونه قرار است برای مسافر اتاق خالی پیدا کند؟
پاسخ معما به این صورت است:
از آنجایی که تمام اتاقهای هتل پر از مسافر است، مدیر هتل از مسافر اتاق ۱ میخواهد تا به اتاق شماره ۲ نقل مکان کند. همچنین از مسافر اتاق ۲ نیز درخواست میکند تا به اتاق شماره ۳ تغییر مکان بدهد.
همینطور مسافر اتاق ۳ به ۴، ۴ به ۵، ۵ به ۶ و ... . در واقع مدیر هتل از مسافر اتاق n تقاضا میکند تا به اتاق n + ۱ برود. از آنجایی که هتل بینهایت اتاق دارد، همواره اتاقی برای انتقال مسافران وجود خواهد داشت. با این کار اتاق ۱ خالی میشود و مسافر جدید میتواند در آن اسکان بیابد.
اگر شب بعد یک اتوبوس ۶۰ نفری برای هتل میهمان بیاید چطور؟ این بار آقای مدیر چه ترفندی برای اسکان مسافران جدید در هتلِ کاملاً پرِ خود به کار خواهد گرفت؟
این دفعه مدیریت هتل از مسافر اتاق ۱ میخواهد تا به اتاق ۶۱ برود. همینطور مسافر اتاق ۲ به اتاق ۶۲، ۳ به ۶۳، ۴ به ۶۴ و ... . به این ترتیب ۶۰ اتاق اول هتل خالی خواهند شد. احتمالاً قاعدهی جای دادن n تعداد (متناهی) مسافر در این هتل را حدس زده باشید؛ برای اسکان m مسافر جدید، مسافر اتاق n را به اتاق n+m انتقال میدهیم.
اما اگر شب بعد اتوبوسی با «بینهایت» مسافر جدید از راه برسد، چطور میتوان آنها را در هتلی که حتی یک اتاق خالی هم ندارد جای داد؟
شیوهی حل مسئله این بار به این صورت است که از مسافر اتاق ۱ درخواست میکنیم به اتاق۲ برود، مسافر اتاق ۲ به اتاق ۴، ۳ به ۶، ۴ به ۸ و ... . یعنی مسافران اتاقهای n به اتاقهای ۲n نقل مکان کنند. با این کار اتاقهای ۲n-۱ (فرد) که تعدادشان بینهایت است، آمادهی پذیرایی از بینهایت مسافر جدید خواهند بود.
درک این مسئله و راه حل آن نیز رابطهی تنگاتنگی با درک مسئلهی ۲ در قسمت قبل این مجموعه دارد. دانستن مفاهیم «تناظر یک به یک» و «مجموعههای نامتناهیِ قابل شمارش» به شما در فهم راه حل این مسئله کمک خواهد کرد.
در حقیقت حتی اگر بینهایت اتوبوس که هر کدام بینهایت مسافر دارند هم از راه برسند، میتوان آنها را در هتل جای داد. اثبات این حالت کمی پیچیدهتر از حالات قبلی است و اگر علاقه دارید میتوانید در اینجا و اینجا دربارهی آن بیشتر بخوانید.
۸. چگونه میتوان با استفاده از تختهی دارت، مقدار π (عدد پی) را تخمین زد؟
یکی از جالبترین راهها برای تخمین مقدار π، انتخاب تصادفی نقاط در شکل زیر است.

چنین شکلی را خودتان هم میتوانید با هر ابعاد دلخواهی درست کنید. فرض کنیم شعاع دایره برابر r باشد. در نتیجه قطر مربعی که آن را محاط کرده است برابر ۲r است. با این حساب مساحت دایره πr۲ و مساحت مربع ۴r۲ خواهد بود.
نسبت مساحت دایره به مربع نیز برابر π چهارم میشود. حالا به هر روشی که دوست دارید، به صورت تصادفی نقاطی را بر روی صفحهی فوق انتخاب کنید.
دقت داشته باشید که هیچ عاملی به جز شانس در انتخاب نقاط دخیل نباشد. هر چقدر که تعداد این نقاط تصادفی بیشتر باشد، نسبت نقاطی که درون دایره قرار گرفتهاند به نقاط خارج از دایره (و درون مربع) به عدد π چهارم نزدیکتر خواهد شد. مقدار تقریبی π با استفاده از این روش، اینگونه حساب میشود.

البته باید توجه داشت که صورت مسئله ممکن است کمی گمراه کننده باشد، چرا که در شرایط پرتاپ دارت به سوی بورد، ممکن است عوامل دیگری نیز دخیل باشند که توزیع تصادفی نقطهها بر روی شکل را تحت تاثیر قرار بدهند؛ اما باید در نظر داشت که عنوان معماها صرفاً برای ساده سازی، رساندن مفهوم کلی و جذابتر کردن مسئله طراحی میشوند. صورت مسئله تعریف دقیقتری را ارائه میدهد.
به طور کلی، این نوع محاسبات آماری که با نمونهگیری تصادفی همراه است، به روش مونته کارلو (Monte Carlo method) مشهور است. دربارهی محاسبهی مقدار π به صورت آماری میتوانید در اینجا به مطالعه بپردازید.
تبلیغات متنی
-
ساکشن غبغب چیست و چگونه انجام میشود؟
-
عناوین روزنامههای ورزشی امروز
-
عناوین روزنامههای امروز
-
کلیک ممنوع! برای دریافت کالابرگ، به هیچ لینکی نیاز نیست
-
بهترین مرکز ایمپلنت دیجیتال دندان کجاست؟ معرفی ۱۰ مرکز برتر
-
کاهش سن اختلالات شناختی به ۴۰ سال
-
بهترین دکتر پیکرتراشی در تهران کیست؟ + لیست ۱۰ دکتر برتر
-
لمینت دندان اقساطی +شرایط پیش پرداخت و قسط چیست؟
-
عمل لابیاپلاستی چیست و چه کاربردی دارد؟
-
با آمدن سرگیف، برنامه نقلوانتقالاتی پرسپولیس لو رفت
-
این مرد قزوینی ۱۵۶ بار ازدواج کرده است
-
تصاویری از تعطیلات لاکچری گلر استقلال در دبی
-
هشدار! تا حد امکان رسید کاغذی نگیرید
-
زنم همیشه در مهمانی است، طلاق میخواهم
-
استوری تلخ رسول خادم دل همه را لرزاند
-
فیلم چند نوجوان در اعتراضات اخیر خبرساز شد
-
تصاویر تلخ از دریاچه ارومیه در زمستان ۱۴۰۴
-
دو روایت از تجمعات اعتراضی در روز یکشنبه
-
مقام اسرائیلی یک پیام تهدیدآمیز فارسی دریافت کرد
-
زمان واریز سود سهام عدالت مشخص شد
-
کنسرت چند خواننده مشهور لغو شد
-
در شبکه خبر اعلام شد؛ ارز تک نرخی میشود
-
مرتضی عقیلی در بیمارستان بستری شد
-
سورپرایز تازه پرسپولیس با جذب لژیونر جوان
-
معادل فارسی واژه «شارژ ساختمان» مشخص شد
-
اولین تلاش ایران برای بازگرداندن منابع مالی از ونزوئلا
-
گل پوشکاشی فولام، لیورپول را زمینگیر کرد
-
هزینه رجیستری آیفون در یک ماه دوبرابر شد
-
از امشب منتظر گرانی ناگهانی برخی کالاها باشید
-
آتش در یک مسجد در مرودشت خبرساز شد
-
پایگاههای نیروی هوایی ونزوئلا نابود شدند
-
اولین عکس رسمی از رئیسجمهور ونزوئلا بعد از بازداشت
-
شهروندان ونزوئلا از ورود تفنگداران دریایی آمریکا خبر میدهند
-
عکسی از زندان مادورو و همسرش در نیویورک
-
رائفیپور پاسخ توهین ایلان ماسک را داد
-
جانشین نیکلاس مادورو مشخص شد
-
رونمایی از تمام حامیان متعصب و مشهور مادورو در تهران
-
پست جدید ترامپ درباره وضعیت ایران
-
ترامپ هدف بعدی خود را بعد از ونزوئلا تعیین کرد
-
خوشحالی مردم ونزوئلا از دستگیری مادورو توسط آمریکا
-
تصویر منتسب به دستگیری مادورو جعلی از کار درآمد
-
آخرین خبر از وضعیت تعطیلی تهران برای فردا
-
پیراهن سرخ برای مدافع استقلال کنار گذاشته شد
-
رویترز: نیکلاس مادورو سقوط کرد
-
وضعیت تعطیلی یکشنبه در تهران نامشخص ماند
بانک اطلاعات مشاغل تهران و کرج
-
سالن های آرایش و زیبایی
-
پزشکان پوست و مو
-
آموزشگاه آشپزی در تهران
-
گالری پوشاک
-
اخذ ویزا
-
کاشت ناخن
-
محصولات پزشکی
-
تدریس خصوصی
-
مزون و شوی لباس
-
اعزام دانشجو
-
خدمات آرایشی و زیبایی
-
خدمات درمانی
-
مدارس
-
طلا و جواهر و زیورآلات
-
صرافی
-
محصولات آرایش و زیبایی
-
خدمات حیوانات خانگی
-
مهد کودک
-
مبلمان
-
سیسمونی و نوزاد
-
مراکز درمانی
-
پت شاپ
-
رستوران و تهیه غذا
-
تعمیرات مبل در تهران
-
خدمات تفریح و سرگرمی
-
پزشکان متخصص
-
باشگاه های ورزشی
-
فست فودهای تهران
-
سرویس خواب
-
موبایل
-
دکتر زنان در تهران
-
فروشگاه ها و لوازم ورزشی
-
کافی شاپ و سفره خانه
-
دکوراسیون داخلی
-
لوازم خانگی
-
دندانپزشکان
-
آموزشگاه ها
-
صنایع غذایی
-
تزیینات داخلی
-
خدمات منزل
-
دندانپزشکی کودک
-
آموزشگاه زبان در تهران
-
تشریفات و موسسه پذیرایی
-
خدمات ساختمان
-
فروش و خدمات خودرو
-
پزشکان زیبایی و لاغری
-
آموزشگاه موسیقی
-
خدمات مجالس
-
قالیشویی در تهران
-
سایر خدمات
-
جراحی بینی و زیبایی
-
آموزشگاه هنری
-
آتلیه عکاسی
-
آژانس مسافرتی و هتل




















نظر کاربران
توی مسئله ی هشت یه اشتباه دارید.
نوشتید شعاع دایره r هست پس قطر مربع 2r هست. احتمالا منظورتون از قطر مربع ضلغ بوده چون توی جمله ی بعد مساهت رو حساب کردید.