اینشتین دیدگاه ها را نسبت به جهان تغییر داد (۲)

مجله دیجی کالا: وقتی اینشتین از پنجره‌ی دفتر کارش به بیرون نگاه می‌کرد، تخیل او هسته‌ی اولیه‌ی نسبیت عام را شکل داد. او بعدا گفت: «برای یک لحظه، فکری به سرم زد. اگر کسی آزادانه سقوط کند، وزن خودش را احساس نمی‌کند.» این اتفاق در سال ۱۹۰۷، یعنی دو سال بعد از اینکه نسبیت خاص او تصور ما از زمان و حرکت را بازنویسی کرد، افتاد. نسبیت خاص نشان داد که قوانین طبیعت، تا زمانی که حرکت شما ثابت است و با سرعتی یکنواخت در خط مستقیم حرکت می‌کنید، به چگونگی حرکت شما بستگی ندارد.


ولی در واقعیت، مردم و اجسام به شیوه‌های گوناگونی حرکت می‌کنند. مثل این است که بادکنکی را سوراخ و آن را رها کنید تا به صورت نامنظم و به جهت‌های مختلف حرکت کند. حتی حرکت‌های ساده، مثل چرخش یک کره یا مدار یک سیاره نیز یکنواخت نیست، آن‌ها دائما تغییر جهت می‌دهند و در نتیجه شتاب می‌گیرند. اینشتین می‌خواست نسبیت را به همه‌ی انواع حرکت‌های شتاب‌دار تعمیم دهد، ولی نمی‌دانست چگونه این کار را بکند.

کسی که سقوط آزاد می‌کند، به سمت زمین شتاب می‌گیرد و هیچ نیرویی احساس نمی‌کند. بنابراین اینشتین نتیجه گرفت که گرانش و شتاب دو روی یک سکه هستند. شتاب رو به سوی بالای یک هواپیما، می‌تواند باعث شود که به صندلی بچسبید. درست مثل زمانی که روی زمین هستید و نیروی گرانش به شما وارد می‌شود. این معادله‌ی شتاب-گرانش، توانست گفته‌ی نیوتون مبنی بر اینکه جرم یک جسم (مقاومت اینرسیایی آن به تغییر حرکت)، با وزن آن (جرم گرانشی) برابر است را توضیح دهد. اینشتین نسبیت خاص را بر این اساس که سرعت نور ثابت است، بنا نهاد. او گفت که نسبیت خاص می‌تواند بر این مبنا که جرم گرانشی و اینرسیایی برابر هستند، ساخته شود. اگر او موفق می‌شد، بدین معنا بود که قوانین طبیعت می‌توانند برای ناظران مختلف یکسان باشد.

در اول کار، پیشرفت آهسته بود. ولی در سال ۱۹۰۸، ریاضی‌دانی به نام «هرمن مینکووسکی» (Hermann Minkowski) نشان داد که چگونه نسبیت خاص نیازمند تلفیق فضا و زمان است. در نسبیت خاص، مقیاس‌های فضا و زمان برای ناظران مختلف متفاوت است. ولی مینکووسکی نشان داد که وقتی فضا و زمان تلفیق می‌شوند و فضا-زمان بوجود می‌آید، تعریفی ریاضی بدست می‌آید که همه‌ی ناظران می‌توانند روی آن توافق کنند. برقراری این مختصات‌ نیازمند یک نقطه‌ی شروع است. ناظران مختلف، نقاط شروع متفاوتی را برمی‌گزینند. بنابراین اگر قوانین طبیعت برای همه یکسان باشد،‌ مختصات هر ناظر باید با مختصات ناظر دیگر یکسان به نظر برسد. بنابراین اینشتین تلاش کرد که فرمولی برای تبدیل سیستم مختصات یک ناظر به دیگری پیدا کند و در عین حال همسنگی را بین گرانش و شتاب حفظ کند. در سال ۱۹۱۲، اینشتین متوجه شد که برای رسیدن به هدفش باید هندسه‌ی اقلیدسی را رها کند. فضای واقعی، نمی‌تواند با خط‌ها و زاویه‌های ایده‌آل آن مطابقت پیدا کند. گرانش مختصات را مغشوش می‌کند؛ مثل اینکه تعدادی خطوط موازی چهار خانه بر روی یک صفحه داشته باشید و سپس یک گوی سنگین روی آن قرار دهید؛ خطوط چهارخانه‌ی شما خمیده می‌شوند.


ولی اینشتین مهارت‌های ریاضی را برای دست و پنجه نرم کردن با هندسه‌ی غیر اقلیدسی یاد نگرفت. خوشبختانه دوست دانشگاهی او به نام «مارسل گروسمن» (Marcel Grossmann) می‌توانست به او کمک کند. گروسمن یک ریاضی‌دان بود و با کارهای ریاضی‌دان قرن نوزدهمی به نام «برنارد ریمان» (Bernhard Riemann) بر روی سطوح خمیده آشنایی داشت. او به اینشتین کمک کرد که طرح کلی نظریه‌ی جدید گرانش را بسازد. در آلمانی به آن Entwurf یا پیش‌نویس می‌گویند. ولی یک مشکل وجود داشت، این روش برای بعضی از سیستم‌های مختصات کار می‌کرد ولی به کار همه‌ی آن‌ها نمی‌آمد. اینشتین ناامید شده بود؛ او در آگوست سال ۱۹۱۳ برای فیزیک‌دانی به نام «هندریک لورنتس» (Hendrick Lorentz) نوشت: «هنوز گره‌هایی وجود دارد و باعث می‌شود که این نظریه برای خود من خیلی قابل قبول نباشد.» اینشتین این‌طور ادامه داد که اگر شتاب همسنگ میدان گرانشی باشد، همه نوع شتاب باید با معادلات گرانش قابل توضیح باشد. اگر نباشد، «نظریه، فرض نخست خود را ابطال می‌کند و بنابراین فاقد پایه و اساس می‌شود.»

دو روز بعد از نوشتن این نامه، اینشتین خوشحال‌تر به نظر می‌رسید. او دوباره به لورنتس نامه نوشت که کمبودهای نظریه‌ی Entwurf جبران شده است. در ماه نوامبر، اینشتین راه‌حل را در نامه‌ای به فیزیک‌دانی به نام «پال ارنفست» (Paul Ehrnfest) توضیح داد و گفت معادلاتی که بتوانند همه‌ی انواع شتاب را توضیح بدهند وجود ندارد. البته این باعث شد که اینشتین نتواند به هدف اولیه‌ی خود برسد. ولی اینشتین خوشحال بود که توانسته بهترین کاری که طبیعت به او اجازه می‌داده است را انجام دهد.

موفقیت غیر منتظره در برلین

اینشتین در شهرهای مختلف زندگی ‌کرد. او سال ۱۸۷۹ در شهر اولم آلمان به دنیا آمد، در کودکی به مونیخ رفت و به هنگام نوجوانی به میلان مهاجرت کرد. آن‌جا از دبیرستان اخراج شد؛ سپس در سوییس به مدرسه رفت و در نهایت در زوریخ از کالج فارغ‌التحصیل شد. او که نتوانست شغل آکادمیک پیدا کند، در سال ۱۹۰۲ در دفتر ثبت اختراعات مشغول به کار شد و سال بعد با دختری به نام «میلوا ماریک» (Mileva Maric) ازدواج کرد.

در طول سال‌ها کار در دفتر ثبت اختراعات، اینشتین توانست مقاله‌های مختلفی بنویسد که فیزیک کلاسیک را در آن‌ها به چالش می‌کشید؛ از جمله کارهایی که در رابطه با نسبیت خاص انجام داد. در نهایت این مقاله‌ها در دنیای فیزیک مورد توجه قرار گرفت و در دانشگاه پراگ برای او قرار ملاقات تعیین کردند. ولی در اولین فرصت به زوریخ، جایی که گروسمن آن‌جا ریاضی درس می‌داد، برگشت. آن‌جا با گروسمن شروع به کار روی نظریه‌ی Entwurf کردند. اینشتین سپس به برلین، جایی که آن زمان قطب فیزیک جهان بود رفت. فیزیک‌دان‌های دانشگاه‌های آن‌جا پیشنهادی به او دادند که نمی‌توانست رد کند. او به لورنتش نامه نوشت: «قرار نیست آن‌جا تدریس کنم. من نمی‌توانم در برابر وسوسه‌ی قبول موقعیتی که باعث می‌شود فقط بتوانم روی نظریاتم تمرکز کنم، مقاومت کنم.»


در تمام این جابجایی‌ها، اوضاع زندگی شخصی اینشتین بدتر می‌شد. او از میلوا جدا شد و با «السا» (Elsa) وارد رابطه شد. میلوا نیز دیگر نمی‌توانست در برلین زندگی کند. در جولای ۱۹۱۴ میلوا دو پسرشان را به زوریخ برد و اینشتین در برلین ماند تا روی نسبیت عام کار کند. در همان سال، کم‌کم تلاش‌های اینشتین شروع به نتیجه دادن کرد. در اواسط سال ۱۹۱۵، او فهمید راهی وجود دارد که می‌توان نسبیت را کاملا عمومی کرد. به جای تلاش بر روی معادلات مربوط به پایستگی انرژی، او بر روی نوشتن معادلاتی که می‌توانستند قانون پایستگی را به کل عالم تعمیم بدهند شروع به کار کرد.

معادلات میدان اینشتین

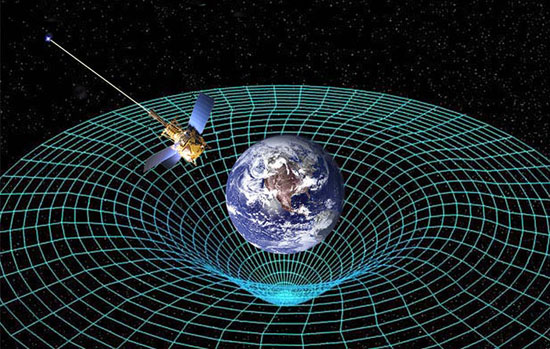
از آن‌جا که جرم و انرژی می‌توانند شکل فضا-زمان را خمیده کنند، هندسه‌ی اقلیدسی نمی‌تواند به خوبی توصیف‌کننده‌ی این پدیده باشد. نسبیت عام اینشتین از ریاضیات پیچیده‌تر هندسه‌ی غیراقلیدسی که در قرن نوزدهم توسط برنارد ریمان ابداع شد، استفاده می‌کند. اینشتین به کمک دوستش مارسل گروسمن، توانست از طریق موجوداتی به نام تانسورها به توصیف بهتری از فضا-زمان برسد. تانسورها مثل بردارها هستند؛ کمیت‌هایی مثل سرعت که از دو جزء تشکیل شده‌اند. (منظور از دو جزیی بودن سرعت، وجود اندازه و جهت برای بردار سرعت است) تانسورها شبیه به آن‌ّها هستند ولی می‌توانند از بیش از دو جزء تشکیل شده باشند. اینشتین از تانسورها برای ساختن معادله‌اش جهت توصیف میدان گرانشی استفاده کرد. توصیفی که بعدا نامش معادله‌ی میدان اینشتین شد.

معادله‌ی میدان اینشتین: Gμν = 8πTμν

در قسمت سمت چپ معادله، تانسوری قرار دارد که توصیف‌کننده‌ی هندسه‌ی فضا-زمان یا همان میدان گرانشی است. سمت راست معادله، تانسوری است که چگالی ماده و انرژی را توصیف می‌کند. یعنی منشاء میدان گرانشی. معادله نشان می‌دهد که هندسه‌ی فضا-زمان با چگالی ماده-انرژی وقتی که با یکاهای صحیح و ثابت‌های عددی تنظیم می‌شود، در ارتباط است.

معادله‌ی میدان اینشتین با لاندا: Gμν + Λgμν = 8πTμν

وقتی اینشتین معادلاتش را به همه‌ی عالم تعمیم داد، فهمید که در این صورت جهان باید بی‌ثبات باشد و به سوی انبساط و یا انقباض برود. برای جلوگیری از این بی‌ثباتی، او عنصری به نام ثابت کیهانی را به معادلاتش افزود که با حرف لاندا نشان داده می‌شود. ثابت کیهانی، نشانگر میزانی ثابت از چگالی انرژی در کل فضا است که باعث می‌شود عالم ثابت و بدون تغییر باقی بماند. شواهد بعدی نشان داد که اتفاقا جهان در حال منبسط شدن است و اینشتین نباید به معادلات اولیه‌ی خود شک می‌کرد. هرچند که به نظر می‌آمد ثابت کیهانی اینشتین دیگر به کار نمی‌آید، ولی در اواخر دهه‌ی ۱۹۹۰ برای توصیف انبساط شتاب‌دار جهان به کار آمد.

حالا او تمام انرژی خود را بر روی ریاضیاتی گذاشت که در سال‌های گذشته آموخته بود و تلاش کرده بود عناصری هندسی به نام تانسورها را فراگیرد. در نوامبر ۱۹۱۵، اینشتین بوی پیروزی را احساس می‌کرد. در ۴ نوامبر، او مقاله‌ای درباره‌ی نسبیت عام به فرهنگستان علوم پروس ارسال کرد. در ۱۱ نوامبر نیز ضمیمه‌ای برای آن فرستاد. هفته‌ی بعد از آن، او مقاله‌ای جدید را این بار به صورت یک سخنرانی آکادمیک ارائه داد. در این سخنرانی، او نشان داد که چگونه خمیدگی فضا-زمان نسبیت عام می‌تواند یک مسئله‌ی بزرگ گرانشی درباره‌ی مدار سیاره‌ی عطارد را حل کند. طی همان هفته، او بالاخره توانست شکل صحیح معادلاتی که میدان گرانشی را توصیف می‌کردند را پیدا کند. نتیجه‌ی آن را در ۲۵ نوامبر ارائه داد. تلاش اینشتین نتیجه داد، نسبیت عام کار می‌کرد.

ادامه دارد…